Strawberry Cream Cake
Fa 1 any
Archive for de desembre 2012
En 1940 se construyó en Tacoma (EEUU) el tercer puente más largo del mundo, con 1600 m de longitud y 850 m en dos soportes. El proyecto original, del ingeniero Clark Elridge, planteaba la construcción de un puente convencional. Pero un grupo de ingenieros encabezados por Leon Moisseiff, ingeniero muy reputado por diseñar en San Francisco, propusieron a los promotores bajaron el coste del proyecto el proyecto utilizando vigas de sólo 2,4 m de ancho, con lo que además se conseguiría que el puente fuera más delgado y elegante. Ese diseño fue el que se llevó a cabo.
El 7 de noviembre de 1940, a causa de un viento de sólo 65 km/h, el puente colapsó a causa de un fenómeno llamado “flameo”. Los torbellinos de aire originados por el viento al atravesar la estructura del puente causaron una oscilación que fue haciéndose cada vez más violenta al entrar en resonancia con la frecuencia natural de oscilación del mismo. Acabo haciendo que se derrumbara el puente.
El 7 de noviembre de 1940, a causa de un viento de sólo 65 km/h, el puente colapsó a causa de un fenómeno llamado “flameo”. Los torbellinos de aire originados por el viento al atravesar la estructura del puente causaron una oscilación que fue haciéndose cada vez más violenta al entrar en resonancia con la frecuencia natural de oscilación del mismo. Acabo haciendo que se derrumbara el puente.
Flameo:
El "PUENTE":
Supongamos que tenemos una tabla de la verdad de una función lógica tal como la que sigue (S es la función y a, b y c las variables de dicha función):
Para expresar S en forma canónica debemos fijarnos en aquellas filas de la tabla en las que S=1. Cada una de estas filas corresponderá a un término de la función. Dentro de cada término, si una variable tiene valor cero deberá negarse. Por contra, si tiene valor uno deberá aparecer sin negar.
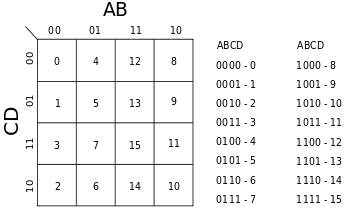
A continuación, colocaremos ceros en las casillas del mapa cuyas coordenadas correspondan con los valores de las variables que producen los ceros de S, también apuntaremos los unos en las casillas restantes.
A continuación hay que intentar realizar agrupamientos de los ceros colocados en el mapa. Nunca en diagonal. Además, los agrupamientos que se hagan hay que tratar que sean lo mayor posible. Los agrupamientos que pueden realizarse en el mapa de más arriba son los siguientes.
La simplificación de la función solo se producirá en los agrupamientos. Es decir, la variable que tenga valor uno aparece de forma directa y la que tenga el valor cero aparece de forma negada respecto a los términos que no se simplifican. Respecto a los que sí se simplifican lo hacen de la siguiente forma:
(EN ESTE CASO LES LETRAS SUBRAYADAS SERÁN LAS NEGADAS)
100 i 110: ABC + ABC= AC
000 I 001: ABC + ABC= AB
000 I 010: ABC + ABC= AC
Como puede verse, se sigue la misma regla que en los términos no simplificados en cuanto a la negación o no de una variable, pero además, cada agrupamiento da lugar a un término en el que la variable que cambia de valor en las casillas del agrupamiento desaparece del término directamente, o sea, no se incluye en él.
La función S simplificada tendrá el siguiente aspecto:
S= AC + AB + AC
Invento, es una técnica, objeto o proceso que posee características novedosas y transformadoras. Sin embargo, algunas invenciones representan una creación innovadora sin antecedentes en la ciencia o la tecnología que amplían los límites del conecimiento humano.
Aquís os cuelgo un vídeo interesante sobre 101 pequeños inventos que fueron revolucionarios.
Aquís os cuelgo un vídeo interesante sobre 101 pequeños inventos que fueron revolucionarios.
Suponiendo que conozcamos la tabla de la verdad de un circuito combinacional, a partir de la cual deseamos diseñar dicho circuito, lo más corriente es tener que buscar una expresión simplificada de la función o funciones a implementar.
Es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2N filas, el mapa K correspondiente debe poseer también 2N cuadrados.
El aspecto de los mapas de Karnaugh es el de la siguiente figura:
En Álgebra booleana, se conoce como término canónico de una función lógica a todo producto o suma en la cual aparecen todas las variables en su forma directa o inversa. Una Función lógica que está compuesta por operador lógico puede ser expresada en forma canónica usando los conceptos de minterm y maxterm.
Toda función lógica es posible expresarla en cualquiera de las dos formas canonicas que existen. Estas dos formas de representación universales son por un lado la forma de maxitérminos o maxterms y por otro lado la forma de minitérminos o minterms. Cada una de estas formas canónicas está formada por un número de términos variable. En cada uno de esos términos deben aparecer todas las variables de la función, ya sea en forma negada o en forma directa (sin negar). Además, en las formás canónicas no existen términos repetidos.
Es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2N filas, el mapa K correspondiente debe poseer también 2N cuadrados.
El aspecto de los mapas de Karnaugh es el de la siguiente figura:
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Karnaugh tendrá 16 celdas, distribuidas en una cuadricula de 4 × 4.
La combinación de dígitos binarios en el mapa representa el resultado de la función por cada combinación de entradas.
En Álgebra booleana, se conoce como término canónico de una función lógica a todo producto o suma en la cual aparecen todas las variables en su forma directa o inversa. Una Función lógica que está compuesta por operador lógico puede ser expresada en forma canónica usando los conceptos de minterm y maxterm.
Toda función lógica es posible expresarla en cualquiera de las dos formas canonicas que existen. Estas dos formas de representación universales son por un lado la forma de maxitérminos o maxterms y por otro lado la forma de minitérminos o minterms. Cada una de estas formas canónicas está formada por un número de términos variable. En cada uno de esos términos deben aparecer todas las variables de la función, ya sea en forma negada o en forma directa (sin negar). Además, en las formás canónicas no existen términos repetidos.
Función NOT:
La porta
lógico NOT es limita a cambiar el señal de On a Off o de Off a On.
La ecuación característica que describe el comportamiento de la puerta NOT es:
Función OR:
La puerta lógica O, más conocida por su nombre en inglés OR (
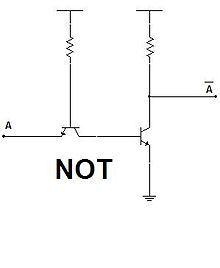
), realiza la operación de suma lógica.
), realiza la operación de suma lógica.
La ecuación característica que describe el comportamiento de la puerta OR es:
Podemos definir la puerta O como aquella que proporciona a su salida un 1 lógico si al menos una de sus entradas está a 1.
Función NOR:
Realiza la operación de suma lógica negada.
La ecuación característica que describe el comportamiento de la puerta NOR es:
Podemos definir la puerta NOR como aquella que proporciona a su salida un 1 lógico sólo cuando todas sus entradas están a 0. La puerta lógica NOR constituye un conjunto completo de operadores.
Función AND:
La puerta lógica Y, más conocida por su nombre en inglés AND (
), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
La ecuación característica que describe el comportamiento de la puerta AND es:
Así, desde el punto de vista de la aritmética módulo 2, la compuerta AND implementa el producto módulo 2.
Función Nand:
realiza la operación de producto lógiconegado.
La ecuación característica que describe el comportamiento de la puerta NAND es:
La ecuación característica que describe el comportamiento de la puerta NAND es:
Podemos definir la puerta NO-Y como aquella que proporciona a su salida un0 lógico únicamente cuando todas sus entradas están a 1.
Función Exor:
realiza la función booleana A'B+AB'. Su símbolo es el más (+) inscrito en un círculo.
La ecuación característica que describe el comportamiento de la puerta XOR es:
|- 
Se puede definir esta puerta como aquella que da por resultado uno, cuando los valores en las entradas son distintos. ej: 1 y 0, 0 y 1 (en una compuerta de dos entradas). Se obtiene cuando ambas entradas tienen distinto valor.
Función Exnor:
La puerta lógica equivalencia, realiza la función booleana AB+~A~B. Su símbolo es un punto (·) inscrito en un círculo. En la figura de la derecha pueden observarse sus símbolos en electrónica. Laecuación característica que describe el comportamiento de la puerta XNOR es:
Se puede definir esta puerta como aquella que proporciona un 1 lógico, sólo si las dos entradas son iguales, esto es, 0y 0 ó 1 y 1 (2 encendidos o 2 apagados). Sólo es verdadero si ambos componentes tiene el mismo valor lógico.
